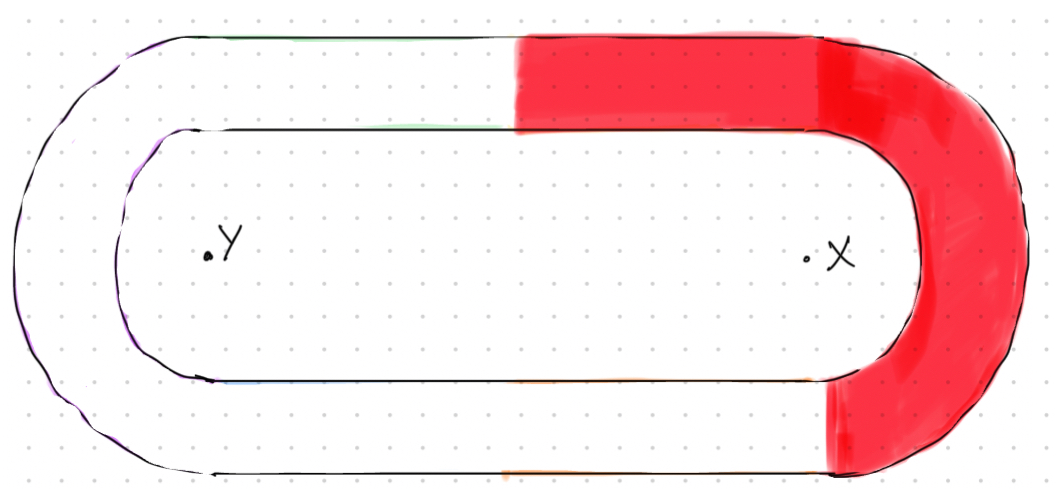
1. DIVIDING THE ELLIPSE INTO SECTIONS

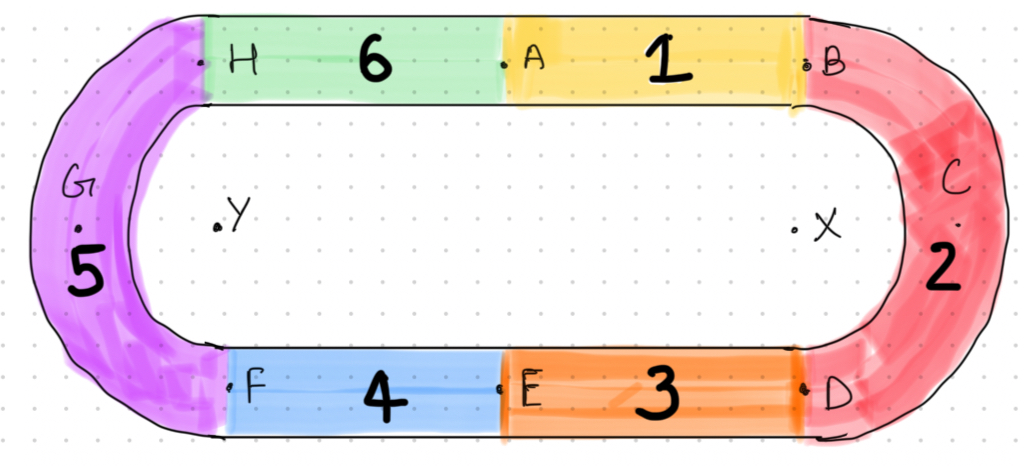
   The progress is to be shown by filling the ellipse. The path of the progress curve is divided into 6 parts:

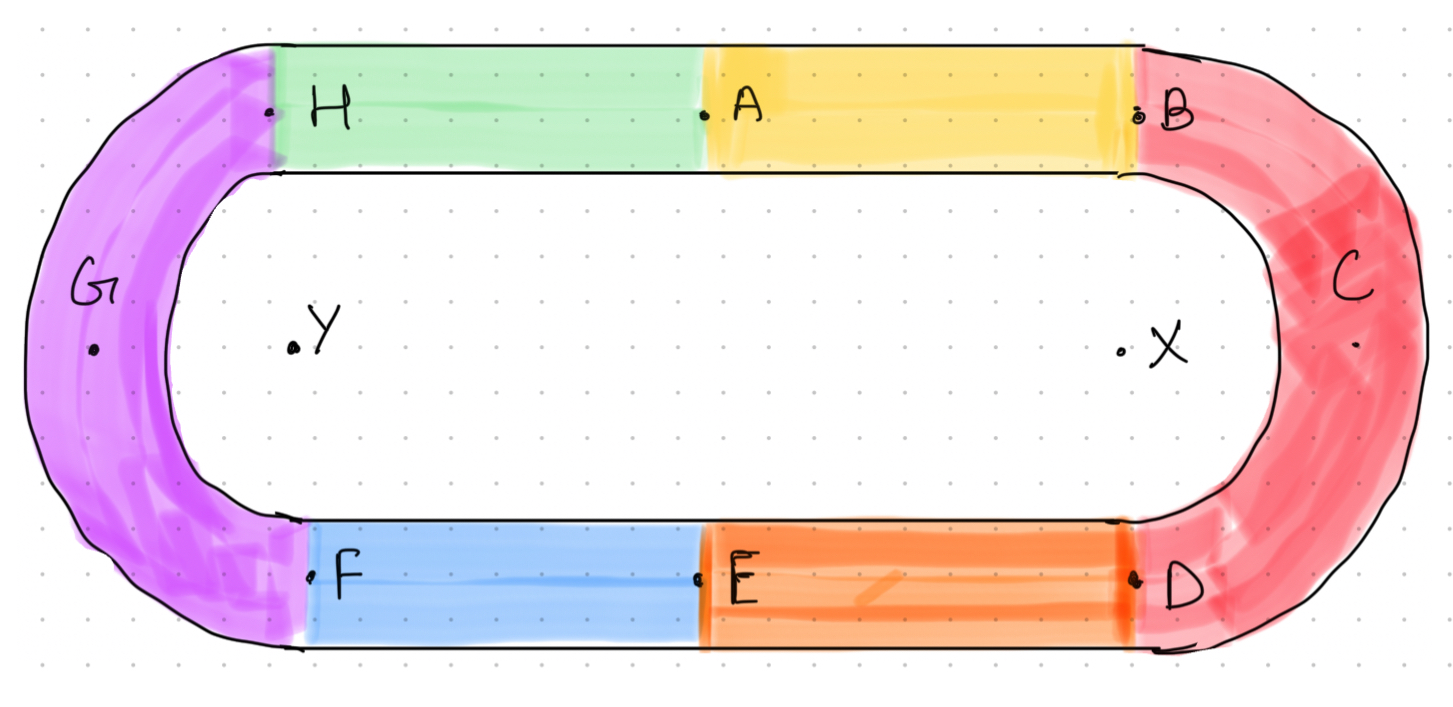
   First line AB First Arc with center X Second line DE Third line EF Second Arc with center Y Fourth line HA

2. CALCULATING THE START AND END POINTS FOR THE ABOVE PARTS

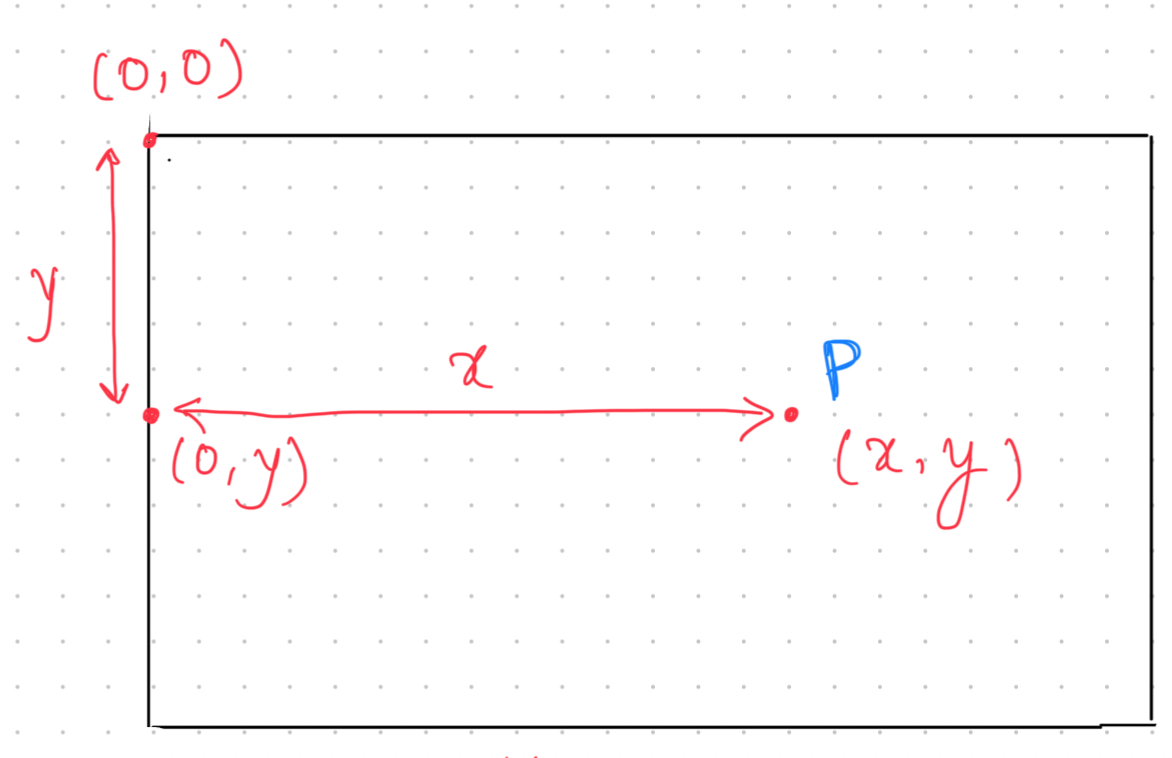
Important before you proceed - For the canvas paint, all coordinate points are calculated keeping the origin on the leftmost screen

For example, a point at a distance of X from the left edge of the screen will have an x-ordinate as X. Similarly, a point at a distance of Y from the top edge of the screen will have a y-ordinate as Y.

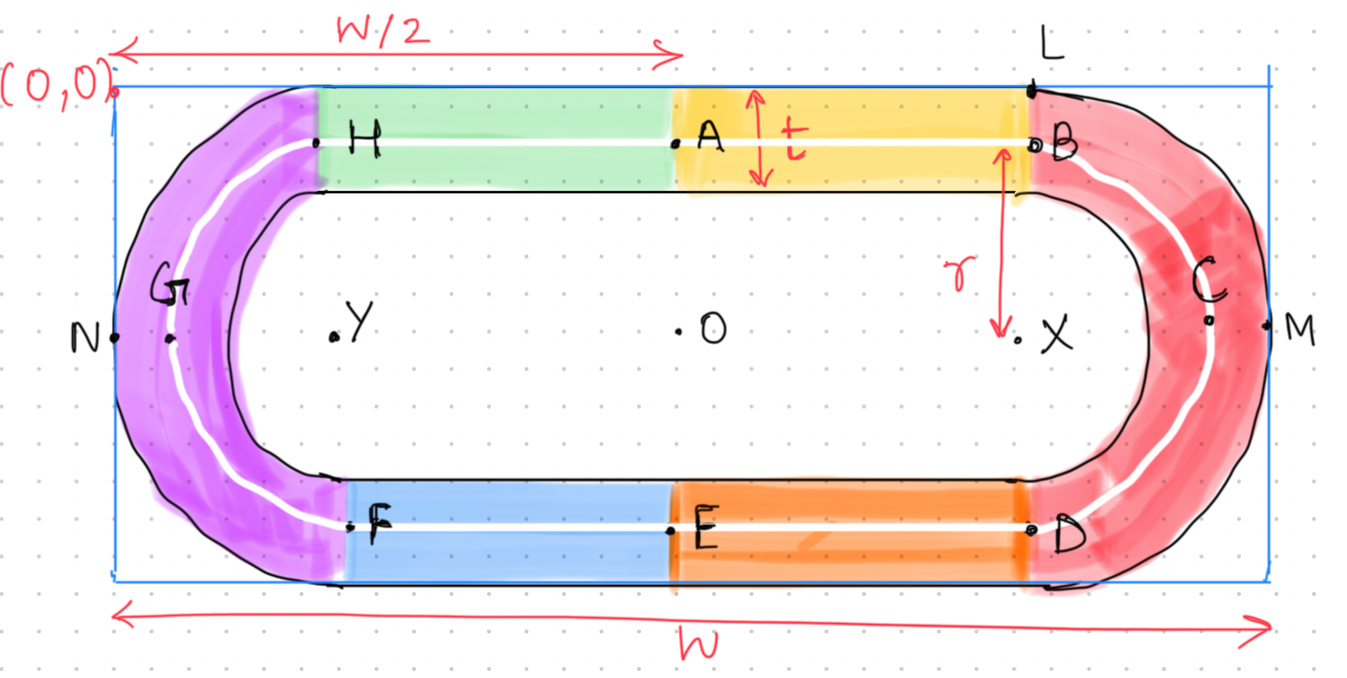
Let the width of the ellipse container be W and the height be H Let the thickness of the ellipse be t

We will be drawing the white path as the progress path. It is the center of the progress loop we need. Giving stroke width t/2 to the purple path will make it fill the ellipse completely.

1. LINE AB

   Then coordinates of the start point A of line AB = (W/2, t/2) ………..(1)

2. FIRST ARC BCD

   Let L be the endpoint on the edge of the first line of the ellipse, L is at the top edge of the screen, hence Ly = 0 Let the center of this arc be X Radius r(XB) = XL - BL = H/2 - t/2 x-ordinate of X = NM - XM = NM - XC - CM = W - r - t/2 Y-ordinate of X = H/2 Therefore (Xx, Xy) = (W - r - t/2, H/2) …………………(2)

3. Second line DE,

   Endpoint E = (A, H - t/2) E = ( W/2, H - t/2 ) …………………(3)

4. For third line EF,

   X-ordinate of F and Y are the same i.e. Fx = Yx Yx = NG + GY therefore Endpoint Fx = NG + GY = r + t/2 Fy = H - t/2 F = (r + t/2, H - t/2) …………………(4)

5. Second arc FGH,

   Center Y = ( r + t/2, H/2 ) …………………(5)

6. Fourth line HA

   To endpoint A = (W/2, t/2), as calculated in (1)

   The ellipse is divided into 6 segments as elaborated above; the progress value needs to be divided into 6 parts to represent an accurate completion fraction.

   Therefore progress = progressValue * 6

   Let progress for each segment be calculated in an array called sections

    int x = (progress / 100).floor();
   var sections = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0];
   for (int i = 0; i < x.toInt(); i++) {
       sections[i] = 1;
   }
   if (x.toInt() <= 5) {
       sections[x.toInt()] = (progress % 100) / 100;
   }
   

VISUALISATION OF THE ABOVE CALCULATION

For a progressValue of 60, progress = progressValue * 6 = 360 x represents the segments that will be filled fully x = Floor(360/100) = 3

sections = [ 1, 1, 1, 0.6, 0, 0 ]

This represents that all the parts need to be filled in the calculated order as follows:

First line AB : sections[0] = 1 means 100% (full) First Arc BCD : sections[1] = 1 means 100% (full) Second line DE : sections[2] = 1 means 100% (full) Third line EF : sections[3] = 0.6 means 60% (partial) Second Arc FGH : sections[4] = 0 means 0% (none) Fourth line HA : sections[5] = 0 means 0% (none)

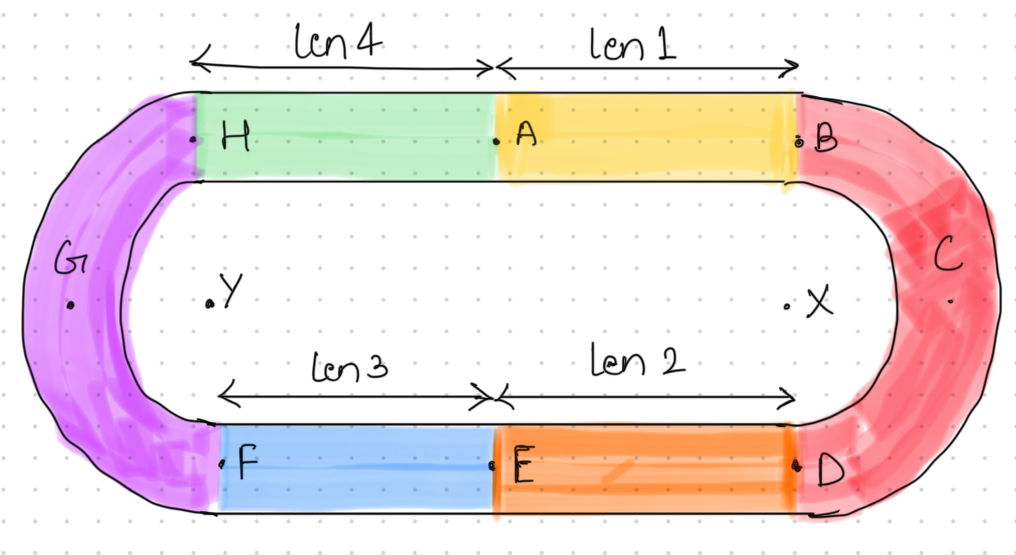
Calculating the lengths of the lines len1 = Bx - Ax; len2 = Dx - Ex = Bx - Ex ( since Bx = Dx as can be seen from fig) len3 = Ex - Fx ; len4 = Ax - Hx;

3. PAINTING Now according to the sections we have calculated and the x value, we paint the canvas. We will paint only the progress amount, which will be calculated as - Length of the part * section value of the part

   Visualization -> For a segment having a section value of 0.6, only 60% of the total length of that segment needs to be filled hence we will paint to only 60% of the total length

   CASE 1: x = 0 -> only first segment is to be painted

   

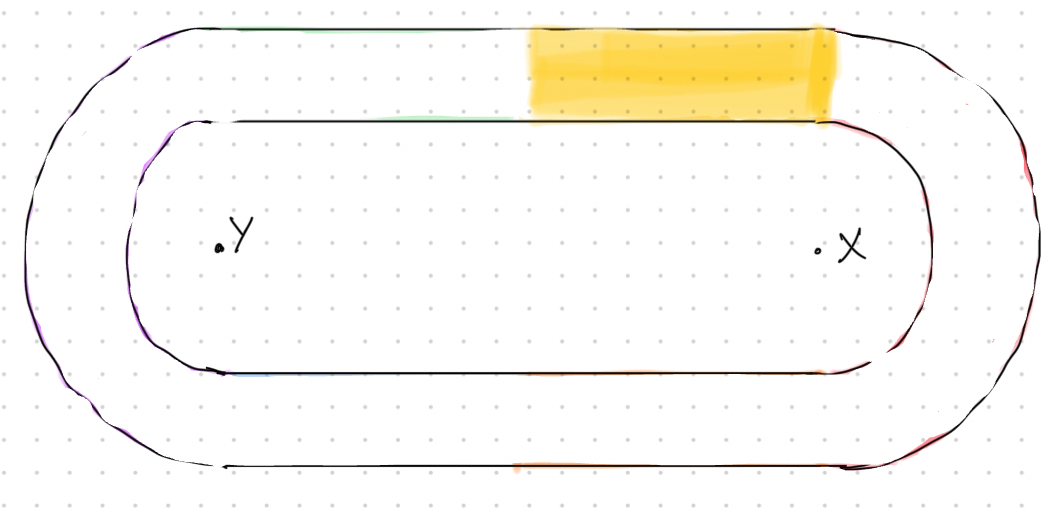
 if (x == 0) {
final path = Path()
..moveTo(startPointX, thickness! / 2)
..lineTo(startPointX + len1 * sections[0], thickness! / 2) //line1;

 canvas.drawPath(path, paint);

CASE 2: x = 1

first segment + first arc is to be painted The full arc is made by painting an arc of 180 degrees. ( -90 to 90 in canvas paint ) Hence progress to be painted for the arc can be calculated as follows - Section value of the arc * 180

Note: math.pi / 180 is multiplied for conversion from radian into degrees

 else if (x == 1) {
final path = Path()
..moveTo(startPointX, thickness! / 2)
..lineTo(firstArcStartX, thickness! / 2) //line1
..arcTo(Rect.fromCircle(center: firstArcCenter, radius: r),
startAngleRad, sections[1] * (180) * (math.pi / 180.0), true);
canvas.drawPath(path, paint);
}

CASE 3: x = 2

first segment + first arc + second line is to be painted

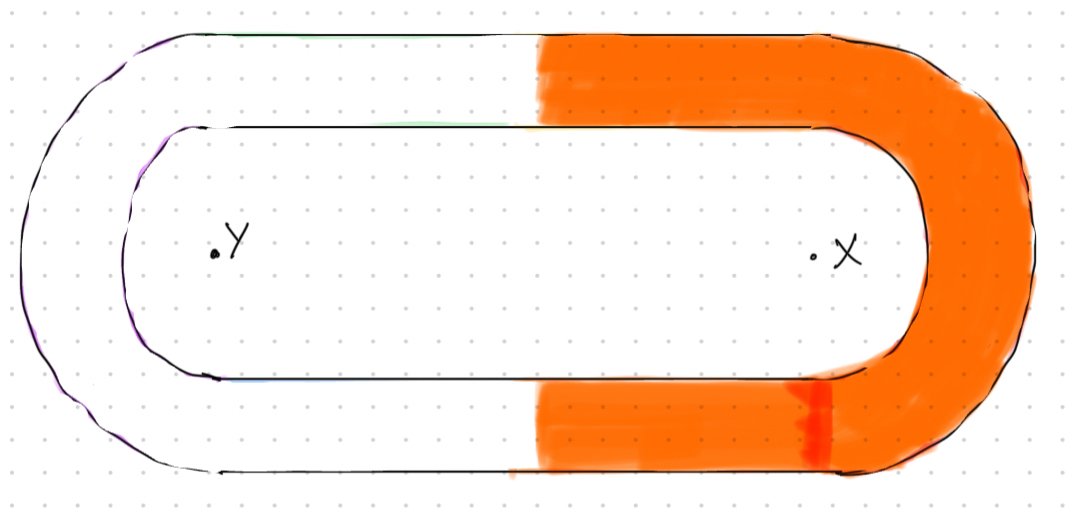
 else if (x == 2) {
final path = Path()
..moveTo(startPointX, thickness! / 2)
..lineTo(firstArcStartX, thickness! / 2) //line1
..arcTo(Rect.fromCircle(center: firstArcCenter, radius: r),
startAngleRad, sections[1] * (180) * (math.pi / 180.0), true)
..lineTo(firstArcStartX - len2 * sections[2],
size.height - thickness! / 2) //line2;
canvas.drawPath(path, paint);
}

CASE 4: x = 3 =>

first line + first arc + second line + third line

 else if (x == 3) {
final path = Path()
..moveTo(startPointX, thickness! / 2)
..lineTo(firstArcStartX, thickness! / 2) //line1
..arcTo(Rect.fromCircle(center: firstArcCenter, radius: r),
startAngleRad, sections[1] * (180) * (math.pi / 180.0), true)
..lineTo(firstArcStartX - len2 * sections[2],
size.height - thickness! / 2) //line2
..lineTo(secondLineEndX - len3 * sections[3],
size.height - thickness! / 2) //line3
;


canvas.drawPath(path, paint);
}

CASE 5: x = 4

first line + first arc + second line + third line + second arc

 else if (x == 4) {
final path = Path()
..moveTo(startPointX, thickness! / 2)
..lineTo(firstArcStartX, thickness! / 2) //line1
..arcTo(Rect.fromCircle(center: firstArcCenter, radius: r),
startAngleRad, sections[1] * (180) * (math.pi / 180.0), true)
..lineTo(firstArcStartX - len2 * sections[2],
size.height - thickness! / 2) //line2
..lineTo(secondLineEndX - len3 * sections[3],
size.height - thickness! / 2) //line3
..arcTo(
Rect.fromCircle(center: secondArcCenter, radius: r),
startAngleRad + piInRadian,
sections[4] * (180) * (math.pi / 180.0),
true);
canvas.drawPath(path, paint);
}

CASE 6: x = 5

first line + first arc + second line + third line + second arc + fourth line

 else {
final path = Path()
..moveTo(startPointX, thickness! / 2)
..lineTo(firstArcStartX, thickness! / 2) //line1
..arcTo(Rect.fromCircle(center: firstArcCenter, radius: r),
startAngleRad, sections[1] * (180) * (math.pi / 180.0), true)
..lineTo(firstArcStartX - len2 * sections[2],
size.height - thickness! / 2) //line2
..lineTo(secondLineEndX - len3 * sections[3],
size.height - thickness! / 2) //line3
..arcTo(
Rect.fromCircle(center: secondArcCenter, radius: r),
startAngleRad + piInRadian,
sections[4] * (180) * (math.pi / 180.0),
true)
..lineTo(thirdLineEndX + len4 * sections[5], thickness! / 2); //line4
canvas.drawPath(path, paint);
}

This is how we will get the ellipse filled with the corresponding progress value. Thanks for reading!